Phase Displacement in Traveling Waves

What This Animation Shows

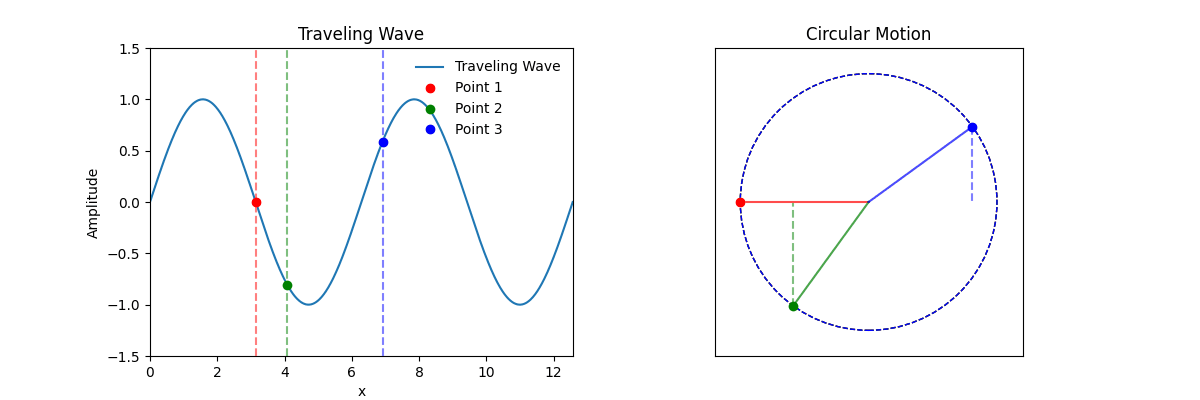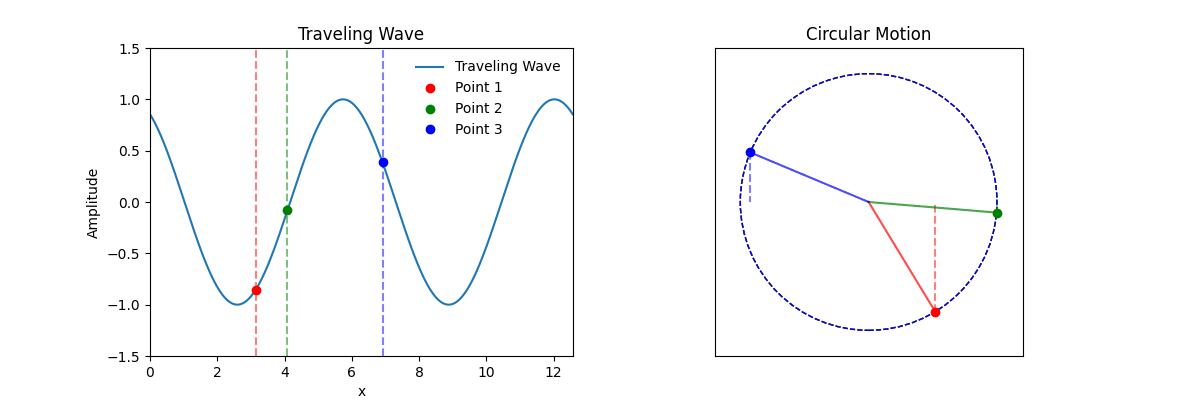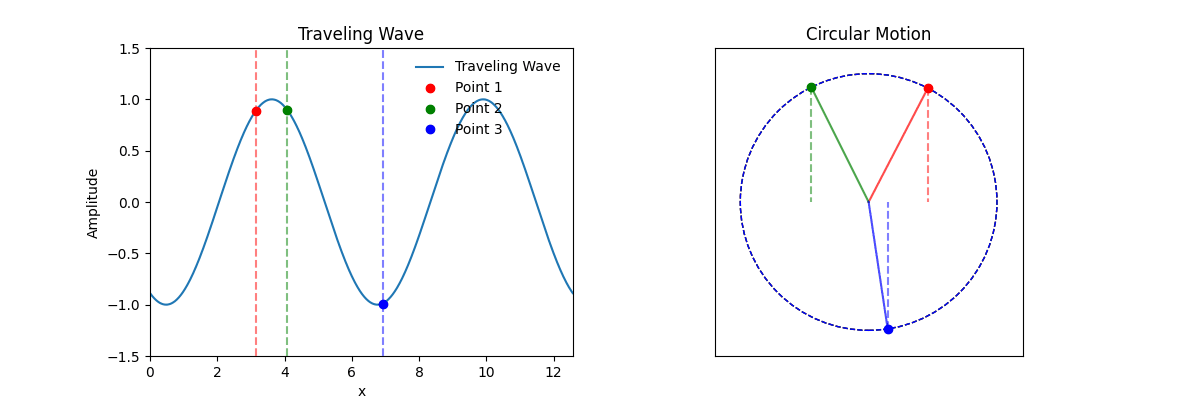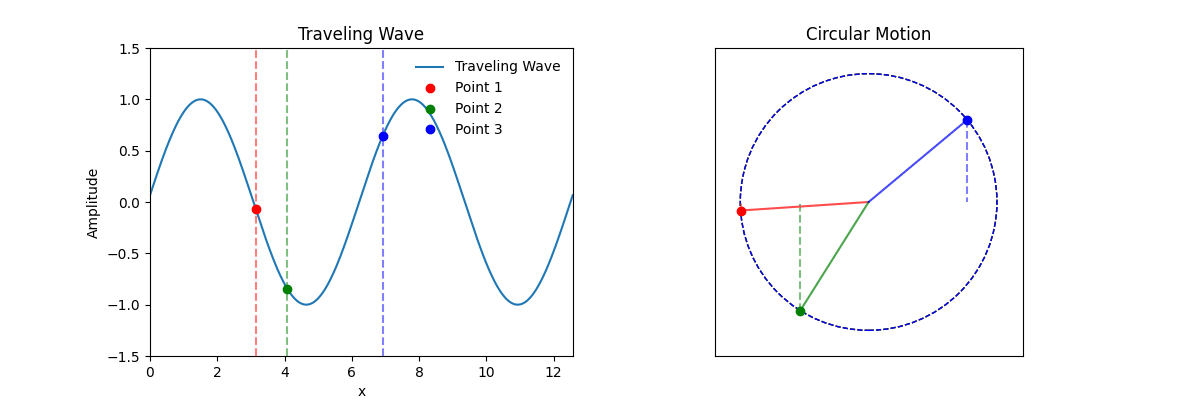
This animation illustrates a fundamental concept in wave physics: the phase of a wave at any given point is a function of both position and time.

Left Panel: Traveling Wave

The left plot shows a traveling wave, typically described by the function:

y(x, t) = A · sin(kx - ωt)

Here, the phase (kx - ωt) depends on both position x and time t. Three points on the wave (red, green, blue) show how displacement changes with time at different fixed positions.

• Each vertical dashed line marks a fixed position along the wave.
• The vertical displacement of each point varies sinusoidally over time, but not synchronously — because the phase depends on where the point is on the wave.

Right Panel: Circular Motion Analogy

The right plot represents each point's motion as a projection of a rotating vector (phasor) around a circle. The angular position around the circle reflects the phase at each location:

• The red, green, and blue vectors rotate at the same angular speed (frequency), but with different initial angles, because each has a different spatial phase offset.
• This helps visualize why even though all points oscillate with the same frequency, they do so out of phase with each other.

Conclusion

The animation shows that in a traveling wave, the phase at each point is not only a function of time, but also of position. This is why the wave form travels through space, rather than oscillating in place.